recursionschemes
Recursion Schemes in Scala
In this piece of work, I want to share some notions about recursion schemes. Recursion schemes are a paradigm based on the abstraction of the recursive steps and the base cases. I will try to provide some justifications about its utilities and a lot of examples where it can be useful. All the examples can be used as scala snippets and feel free to play with it in Scastie, an online scala editor. Enjoy!
Introduction
I’m sure that all of you, in some way, have heard about recursion. The idea of recursion lies in the usage of base definition and some rules to build new structures based on the previous one. In this context, inductive and recursive constructions can be seen as points of view of the same idea. I prefer to talk about induction whenever I talk about data types and recursion referred to functions that traverse inductive types. One of the main examples are natural numbers, in mathematics, and lists in computer science. In both cases we have a base case that tell us an example of an element of our structure and rules to produce new elements. In the case of natural numbers, the base case is 0 is a natural number and for the case of Lists, Nil is a List. The next step is to provide a rule to build, inductively, new numbers and new lists. For the first one we have the basic rule every natural number has a next element and, for lists, every list is Nil or has a head of type A and a tail of type List[A]. A simple implementation of these two types in Scala is:
sealed trait Nat
final object Zero extends Nat
final case class Suc(n: Nat) extends Nat
sealed trait List[+A]
final object Nil extends List[Nothing]
final case class Cons[A](head: A, tail: List[A]) extends List[A]
In both cases we can see the recursive strategy in the Cons and Suc definitions, with an argument defined by its own type.
With every structure builded inductively, there are functions acting on them. Some of these functions are known as recursive functions, which are defined by specifying the image of the base cases and the image of a generic inductive step. For example, lets define the length of a list:
def length[A]: List[A] => Int = {
case Nil => 0
case Cons(h, t) => 1 + length(t)
}
We must read this definition as: if the given list is Nil, its length equals 0 and, suposed we know the length of the tail, this value plus one gives the full length of the list. Indeed, we can follow every step in the recursive calls to find the length of a given List.
With these examples we can observe two behaviors:
1) Every inductive structure uses its own type to define the rule to build the next iteration.
2) Every recursive function with domain an inductive data type needs to traverse the structure until the base case and them iterates to produce the result.
These observations are pretty well defined over the previous examples. But, in general, the definition of recursive functions needs to use the recursive calls in some key points and, in so many cases, these points are not so clear. This may cause errors during the definition of recursive functions. For this reason, it would be interesting to have a clear separation between the recursion step and the base cases. In fact, what we will try to build is a blueprint for general recursion. The shape of this blueprint can be resumed as:
1) Give me a functor F[A] and a way to evaluate it for a fixed type B (think in the evaluation of an expression to an integer). F[A] will represent a general inductive step, but without any reference to previous cases. The role of the evaluation can be seen as a single step of the recursive function.
2) I have a magic type constructor to turn F[A] into its associated inductive type and a way to lift the base case evaluations to an evaluator that traverse the inductive type.
This blueprint, together with the inductive type constructor and the lifter operator is what is called recursion schemes. Lets develop these ideas.
Functors, F-algebras and Fix
As we have told before, we want to build an abstraction of general recursion. I will try to build all these ideas over an example, to keep the focus on the intuition. Lets start with a simple example. Imagine we want to implement the ring structure of the set of integers, i.e. , the set together with multiplication and addition. A simple implementation of this type would be:
sealed trait Ring
case object Zero extends Ring
case object One extends Ring
case class Elem(x: Int) extends Ring
case class Add(x: Ring, y: Ring) extends Ring
case class Mult(x: Ring, y: Ring) extends Ring
Of course, the Zero and One can be used interchangeably with Elem(0) and ELem(1), but we prefer to keep these two elements as special, because they are the neutral elements of addition and multiplication.
As we said before, we want to separate a general step from the inductive steps. For this purpose, let’s imagine that we have a base type A and we want to implement sum and product operations of just two elements of that type. It can be defined in Scala as:
sealed trait RingF[+A]
case object Zero extends RingF[Nothing]
case object One extends RingF[Nothing]
case class Elem(x: Int) extends RingF[Nothing]
case class Add[A](x: A, y: A) extends RingF[A]
case class Mult[A](x:A, y: A) extends RingF[A]
Because of the inductive rules of Ring, we can build a value as deep as we want, for example:
val expresion1 = Mult(Elem(4), Add(Elem(3), One))
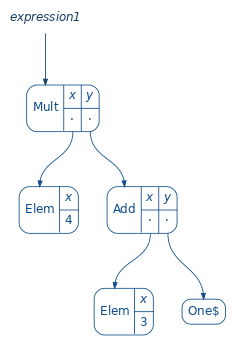
But, for RingF, we are able to build just base cases like Elem(7), Add(3, 4), etc.
Imagine that we want to evaluate the expressions produced by Ring and RingF, for example, the value resulting from solving the operations. For Ring, this can be made by the recursive function:
def toInt: Ring => Int = {
case Zero => 0
case One => 1
case Elem(x) => x
case Add(x, y) => toInt(x) + toInt(y)
case Mult(x, y) => toInt(x) * toInt(y)
}
And, in Case we want to define it for RingF we can simply solve it without recursive calls:
def evalToInt: RingF[Int] => Int = {
x => x match {
case Zero => 0
case One => 1
case Elem(x) => x
case Add(x, y) => x + y
case Mult(x, y) => x * y
}
}
We can observe that, obviously, is simpler to write evalToInt than toInt. Don’t forget our main goal, an abstraction to transform the simpler fuction into the (a bit) complex one.
Here is where the magic comes, if we want to evaluate, for example, a value of the form RingF[RingF[A]], i.e., an expression of deeph two, we need first an evaluation of the form RingF[RingF[A]] => RingF[A] and then, another evaluatuion RingF[A] => A. In the previous example, A is Int. The way of doing this is based on a good property of RingF: it is a functor. A functor, for our porpouses, is a type constructor with the property that we can implement a way of translating functions between types in functions between the constructed types. So for this simple example, for every type A we can build a new type RingF[A]. Now, given a function f: A => B, we know how to build a function with the signature map: RingF[A] => RingF[B]. This can be easily define and implemented in Scala:
trait Functor[F[_]] {
def map[A,B](f: A => B): F[A] => F[B]
}
val ringFunctor = new Functor[RingF] {
override def map[A, B](f: A => B): RingF[A] => RingF[B] = {
case Zero => Zero
case One => One
case Elem(x) => Elem(x)
case Add(x, y) => Add(f(x), f(y))
case Mult(x, y) => Mult(f(x), f(y))
}
}
We can summarize the functor behaviour in the following image:
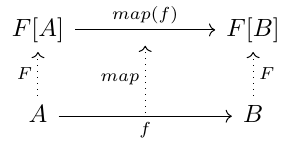
For RingF, we simply encapsulate the image of f under the RingF constructor. Now that we know how to lift functions using the map property of the functor, we can lift the one step evaluation evaltoInt into an evaluation between RingF[RingF[A]] => RingF[A] by simply taking map with A as RingF[A] and B as A :
def liftInt: RingF[RingF[Int]] => RingF[Int] = {
ringFunctor.map(evalToInt)
}
So, thanks to the map property, we know how to lift one floor of recursion our base cases. Using this, we can evaluate a two floor of recursion by simply reading the signature of our functions. The function able to evaluate this is evalToInt(map(evalToInt)(_)) because of the following picture:
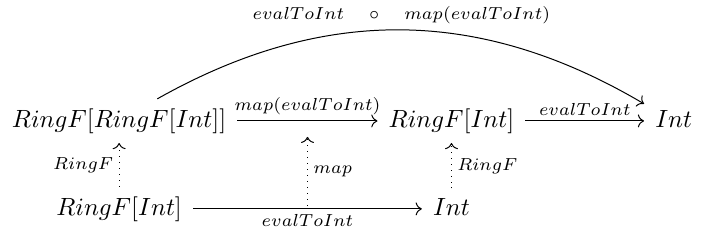
Our goals now are to define the full inductive expression of RingF and lift evalToInt to the infinite floor of recursion.
Before digging into recursion, lets set some terminology. Given a functor F, any function with signature F[A] => A is called an F-algebra over A. A natural question can arise from this: why on earth is this called algebra?. In mathematics, very roughly speaking, an algebra is a set A and a set of operations acting on it. The only requirement over this operations is that it should be closed in A, i.e., if we apply a finite number of operations, the result is an element of A. For example, the integers forms an algebra (even more, it is a ring) with the operations of product and addition. Now, the concept of F-algebra is a generalization of this idea, because the functor is defining the set of operations (Add, Mult for our RingF) and the function F[A] => A is defining the laws of solving the operations. For the case of integers, this is encoded in the function evalToInt. So, we can conclude that there is the same information in the evalToIntfunction and in the algebra of integer numbers.
After this explanation, lets go back to recursion. The argument to do this can be formally made in terms of initial objects of certain categories, but let me try to focus on the main ideas rather than the technical details.
If we want to find the full inductive behind RingF type that’s mean that we don’t care about the depth of the expression of our ring, so we can think about it as a type H related to ring[A] and with an infinite depth. It’s obvious that an object with this property must verify, in some sense, that ring[H] = H, read as: if we are in a full general inductive step, we don’t get nothing if we repeat the application of RingF. So, we can rephrase the equality as: All the information inside ring[H] is inside H and the converse is also true. The equality understood as this property is called an isomorphism between the types H and RingF[H]. This is why we prefer to call H as Fix[RingF] because it is a fixpoint of the equation RingF[X] = X. So the final signature is Fix[RingF] = RingF[Fix[RingF]]. Avoiding the formal and technical proofs, we can just implement the previous definition. Even more, this argument works for every Functor F[A], so we can simply write an abstraction like:
case class Fix[F[_]](value: F[Fix[F]] )
object Fix {
def fix[F[_]](ff: F[Fix[F]]): Fix[F] = new Fix[F](ff)
def unfix[F[_]]: Fix[F] => F[Fix[F]] = f => f.value
}
fix and unfix defines the way of translating information back and forth (these functions defines the isomorphism of the fixpoint).
Now, we can build our inductive type Ring by simply fixing the RingF functor:
type Ring = Fix[RingF]
val zero = Fix[RingF](Zero)
val one = Fix[RingF](One)
def elem: Int => Ring = x => Fix[RingF](Elem(x))
def add: (Ring, Ring) => Ring = (x, y) => Fix[RingF](Add(x, y))
def mult: (Ring, Ring) => Ring = (x, y) => Fix[RingF](Mult(x, y))
and we can build recursive values like:
val expresion2 = mult(elem(4), add(elem(3), one))
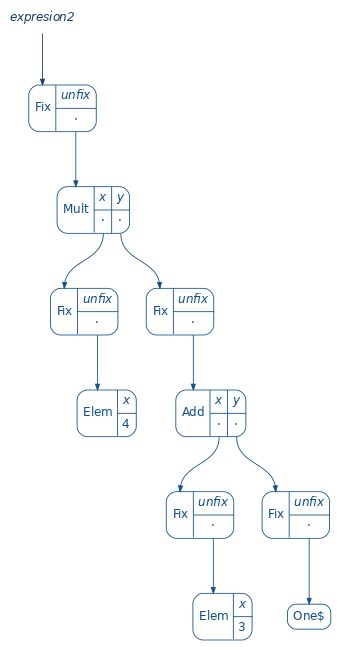
Yow can compare this with expression1.
We actually have reached the first goal, i.e., to find an inductive abstraction for our starting functor RingF. What its left is to take our way to evaluate this data type starting with our evalToInt function.
Catamorphisms
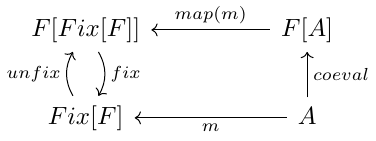
If we take a fast recap, what we have is a functor RingF and our Fix that can transform our functor into an inductive data type. The Fix[_] type constructor has two functions, called fix and unfix that, as we already said, defines the type equality (isomorphism) Fix[F] = F[Fix[F]]. Our goal now is to transform our algebra evalToInt: RingF[Int] => Int into a function that can traverse our inductive data type. This is equivalent to find a function m: Fix[RingF] => Int out of evalToInt. More generally, we can represent this idea for every functor and every algebra eval: F[A] => A. Lets make a simple diagram that represent all this ideas
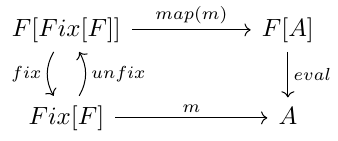
Looking at this diagram, if we want to define m we only need to read the diagram and composing the functions, i.e., taking m as eval o map(m) o unfix. But, to understand it better, let’s see first the case of RingF and evalToInt:
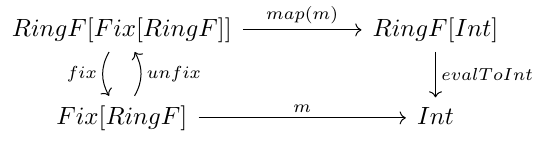
In this case, the recursive call comes from map(m), because m is the function we are defining. We can implement such a function as
def cata: Fix[RingF] => Int = {
x => evalToInt(ringFunctor.map(cata)(Fix.unfix(x)))
}
val exp1 = mult(elem(4), add(elem(3), one))
cata(exp1)
res: Int = 16
We can follow each step of recursion in the following gif:
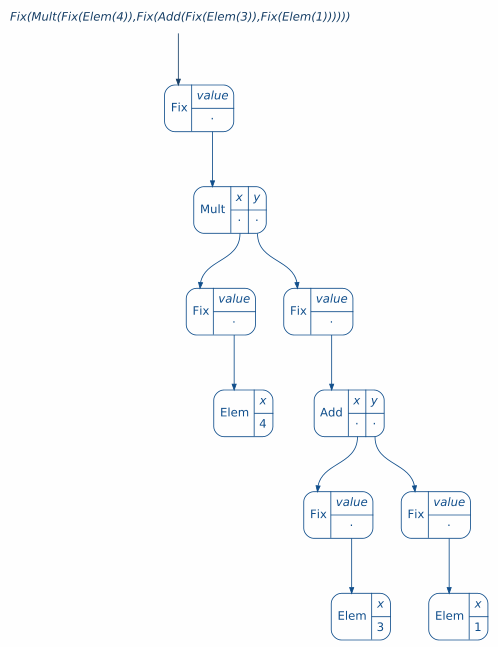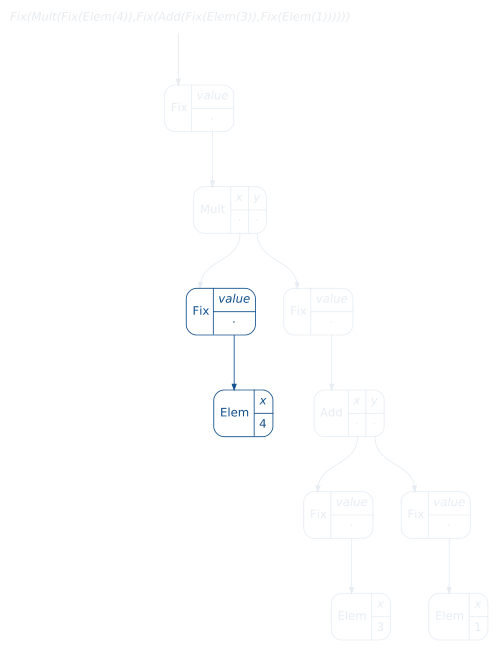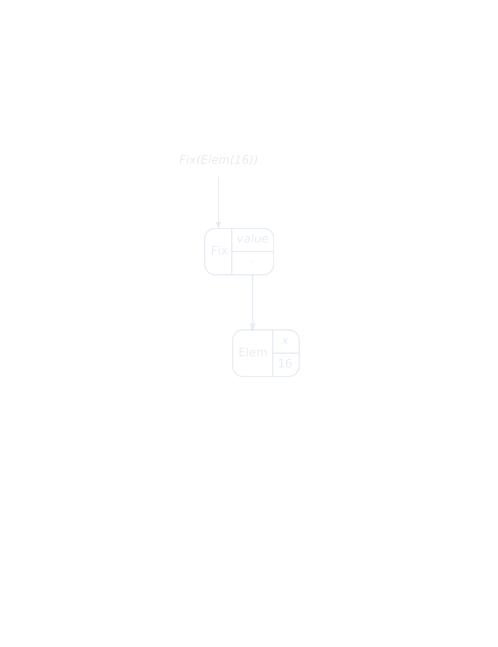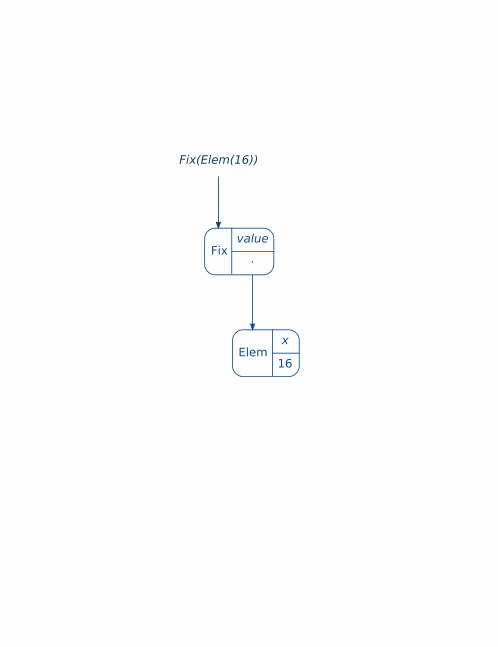
So we are done! We achive our goal of lifting evalToInt to our recursive data type Ring. But, our implementation of cata looks pretty concrete for this case. As we can see in our first diagram, we can do this for any functor and for any evaluation, i.e, any algebra over it. Let’s do this in the same way, by reading the diagram.
def cata[F[_], A](alg: F[A] => A)(implicit F: Functor[F]): Fix[F] => A = {
x => alg(F.map(cata(alg))(Fix.unfix(x)))
}
And, with this, we can call it by typing cata(evalToInt)(ringFunctor)(exp1). One of the best properties of this way of building recursion is that there is no direct dependence between the algebra and recursion. All the steps required to traverse the structure are under the hood, so we don’t need to worry about recursive calls, we only need to define our algebra in the most simple way.
One note about terminology: the name cata comes from catamorphism, which etymology comes from Greek and is the composed word cata, wich means “downwards”, and morphism, wich can be translated as “shape”. So, this name fits very well with its behaviour.
Lists and folds
At the very beginning, we talk about Lists as an essential example of recursive data type. There is as well one basic operation over Lists implemented in scala called foldRight. What this function does is to traverse the List structure by evaluating a function with a starting value. Lest see an example of this:
val l1 = List("a", "b", "c")
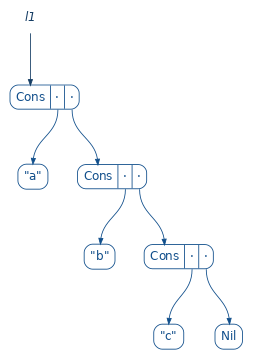
l1.foldRight(0)((n, t) => n + 1)
res44: Int = 3
We need to read foldRight as: start with 0 and apply the function given while our next element is not Nil. The function above computes the length of l1. If we look carefully, this function looks pretty similar to cata, where our algebra is the function acting over the base cases. Let’s translate all of this using Fix and cata. First, lets define the functor associated with List. To make it simple, we’re gonna deal only with List[String] to avoid type parameters.
sealed trait ListF[+A]
case object NilF extends ListF[Nothing]
case class ConsF[A](head: String, tail: A) extends ListF[A]
And now, we can turn this ListF into a functor by implementing map:
val listOfStringFunctor = new Functor[ListF] {
override def map[A, B](f: A => B): ListF[A] => ListF[B] = {
case NilF => NilF
case ConsF(h, t) => ConsF(h, f(t))
}
}
Using Fix we can build our own version of l1:
type ListString = Fix[ListF]
val nil = Fix[ListF](NilF)
def cons : (String, ListString) => ListString = (h, t) => Fix[ListF](ConsF(h, t))
val fixL1 = cons("a", cons("b", cons("c", nil)))
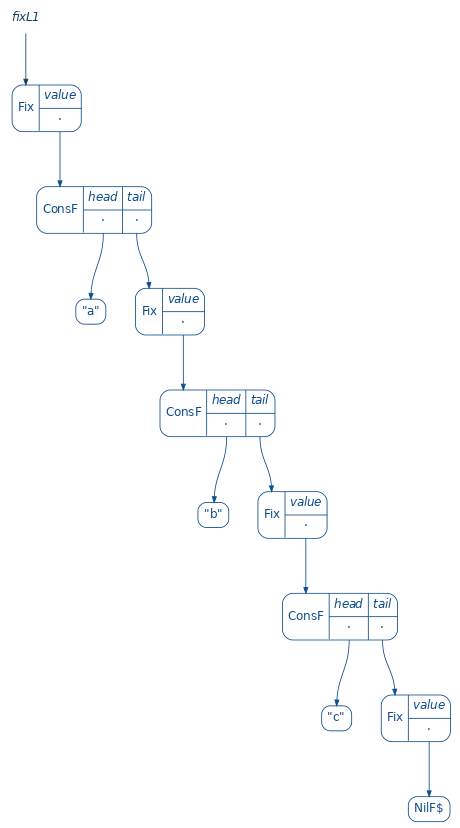
Finally, let’s try to implement foldRight using cata:
def myFoldRight[A](baseValue: A)(evaluator: (String, A) => A)(l: ListString): A = {
def alg: ListF[A] => A = {
case NilF => baseValue
case ConsF(h, t) => evaluator(h, t)
}
cata(alg)(listOfStringFunctor)(l)
}
myFoldRight(0)((x, y) => y + 1)(fixL1)
res35: Int = 3
We have built the foldRight method of List[String] in terms of cata, but we can go further. It turns out that foldRight is as useful as cata in the sense that foldRight recreates general recursion. The main idea is: every recursive function over an inductive data type can be defined as a foldRight. So, this is the same as cata. The reason of this is that we can translate cata (in some sense) into foldRigth. Lets do this in our main example Ring:
def foldR[Z](e: Fix[RingF])(elem: Elem => Z)(add: (Z, Z) => Z)(mult: (Z, Z) => Z): Z = {
e.value match {
case Elem(x) => elem(Elem(x))
case Add(x, y) => add(foldR(x)(elem)(add)(mult), foldR(y)(elem)(add)(mult))
case Mult(x, y) => mult(foldR(x)(elem)(add)(mult), foldR(y)(elem)(add)(mult))
}
}
Of course, we can recreate evalToInt using this by writing:
exp: Ring = Fix(
Add(
Fix(Add(Fix(Elem(3)), Fix(Elem(3)))),
Fix(Add(Fix(Elem(3)), Fix(Elem(3))))
)
)
foldR[Int](exp)(x => x.x)((x, y) => x + y)((x,y) => x * y)
res61: Int = 12
To justify that this is equivalent to cata(evalToInt)(a), lets do some reasoning about the signature of this function. First of all, the signature of foldR is:
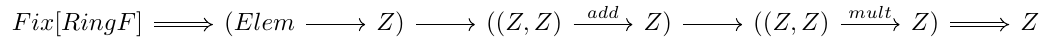
And, using currying, we can turn this last expression into
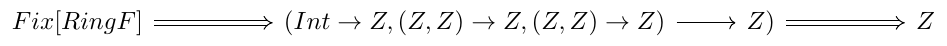
And, finally, the signature of this triplet can be understood in Scala as a trait. In fact, this has the signature of our algebra:
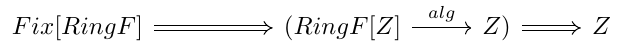
And, of course, reading the composition of arrows we get the shape of cata:
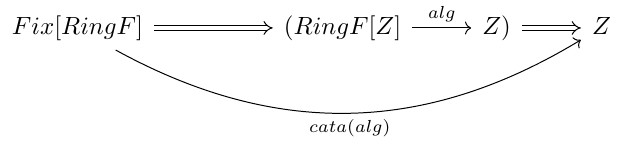
So, as we have already see, foldR is exactly the same idea as cata, but in a more explicit way. In both cases, we have a general abstraction of recursion.
A philosophical interpretation of folds and cata
What we can conclude at this point is that cata is the abstraction of recursion. In some sense, the inductive type Ring is a set with elements inside it in form of expressions. On the other hand, cata is a way of transforming evaluations of operations into real evaluations of exapressions. So, in some sense, cata is a way of looking at Ring, i.e, cata produces an observation of Ring for every algebra. A natural question can arise from this point: if we know all the observations of an inductive type, can we know everything about that type? The answer is affirmative and is one of the motivations of cathegory theory. Let’s build this equivalence for our example. We want to build an equivalence, in the same sense as we did with the equality Fix[RingF] = RingF[Fix[RingF]] and the pair fix and unfix. To do this, we need to build two functions with shape
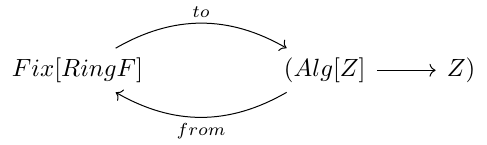
and with the property that both compositions produces the identity function. Alg[Z] is an abbreviation for the signature RingF[Z] => Z. As we said before, this pair of functions with this property is called an isomorphism and we can write this signature in Scala as:
trait Iso[A, B] {
def to(a: A): B
def from(b: B): A
}
So we need to implement an Iso between Fix[RingF] and something that represents the functions of type Alg[Z] => Z. We can wrap this last type in a trait
type Alg[Z] = RingF[Z] => Z
trait BBEnc {
def apply[Z](alg: Alg[Z]): Z
}
So, our goal is almost done, the to arrow is cata by simply observing the diagrams of the last section and, to build from, we only need to fix the objects while we are traversing the structure in the observations of BBEnc. All can be summarized in the following implementation of Iso[Fix[RingF], BBEnc]:
val RingIso = new Iso[Fix[RingF], BBEnc] {
override def to(expr: Fix[RingF]): BBEnc = {
new BBEnc {
override def apply[Z](alg: Alg[Z]): Z = {
cata(alg)(ringFunctor)(expr)
}
}
}
override def from(enc: BBEnc): Fix[RingF] = {
def myAlg: Alg[Fix[RingF]] = {
case Zero => Fix[RingF](Zero)
case One => Fix[RingF](One)
case Elem(x) => Fix[RingF](Elem(x))
case Add(x, y) => Fix[RingF](Add(x, y))
case Mult(x, y) => Fix[RingF](Mult(x, y))
}
enc.apply(myAlg)
}
}
Finally, we can check the indentity of the composition with our expression1
RingIso.from(RingIso.to(expression1)) == expression1
---
res73: Boolean = true
As a conclusion, we can interpret inductive types as the set of all observations (evaluations) of a certain functor, i.e, the evaluation of algebras. This is, in fact, an application of a very deep result called the Yonneda lemma, in cathegory theory. In this particular case, these interpretations are known as the Böhm-Berarducci encoding for the System F lambda calculus. This encoding explains the name of our type BBEnc.
F-coalgebras and Anamorphisms
If we think about the cata(evalToInt) function, what this function does is to reduce a tree of operations into an Integer. Imagine that we want to do some converse function, i.e., a function that takes an Int and produces an element of Ring. The signature for this function would be Int => RingF[Int]. In a more general case, we can take any fixed type A and any functor F and write A => F[A]. Functions with the previous signature are called F-coalgebras, because of duality with F-algebras.
To provide an example of this kind of function, we can use a function that, given an integer, produces the expression of products of its factors. As we have done before, let’s do this for a base case (just splitting our number in a product of two others) and then we will try to lift this function to produce the full factorization of the given number.
For the base case, we can write:
def findDivisorsOf(r: Int): RingF[Int] = {
def loop(n: Int): RingF[Int] = {
n match {
case 0 => Zero
case 1 => One
case x =>
if (x >= r) Elem(x)
else if (r%x == 0) Mult(r/x, x)
else loop(n+1)
}
}
loop(2)
}
For example, findDivisorsof(6) produces res55: RingF[Int] = Mult(3, 2), but for findDivisorsof(12) we only get res55: RingF[Int] = Mult(6, 2) and we may want to keep factorising the 6 as Mult(3, 2). To do this, we need to produce a new diagram that represents the idea of lifting this function to the Fix of RingF. This can be done by reading our first diagram, but reversing the arrows:
And, as we did before, we only need to read this diagram to get an implementation. The direct implementation, following the same arguments as with catais:
def ana[F[_], A](coalg: A => F[A])(implicit F: Functor[F]): A => Fix[F] = {
x => Fix((F.map(ana(coalg))(coalg(x))))
}
As you can see, this new lifter function is called ana. This name comes from the greek word anamorphism, which is the composition of the word ana(“upward”) and, morphism(“shape”). Of course, the meaning of this word is dual with catamprphism.
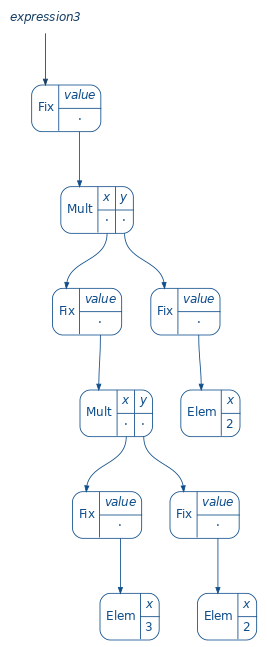
At this moment, all we need to do is to call ana(findDivisors)(ringFunctor)(n) to get a full expression that represents the factorization of n. For example:
val expression3 = ana(findDivisorsOf)(ringFunctor)(12)
expression3: Fix[RingF] = Fix(
Mult(Fix(Mult(Fix(Elem(3)), Fix(Elem(2)))), Fix(Elem(2)))
)
Hylomorphisms
Now,,we can build expressions from integers using anaand know how to reduce it using cata. We can combine both to get a new evaluator by reading the direct diagram:
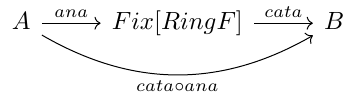
The new function (ana o cata) is called hylomorphism and is pretty useful. For example, we can use it to check that our findDivisorsOf and evalToInt raise the starting value if we did one after another:
def hylo[A, B, F[_]](ev1: A => F[A])(ev2: F[B] => B)(implicit functor: Functor[F]): A => B = {
x => cata(ev2)(functor)((ana(ev1)(functor)(x)))
}
hylo(findDivisorsOf)(evalToInt)(ringFunctor)(12)
---
res40: Int = 12
It works! Let’s try to implement a more fancy function. For example, let’s write a simple function to represent the factorization of an integer as a String. To do this, we need first a prettyPrint function and then apply hylo to it with indDivisorsOf.
def prettyPrint: RingF[String] => String = {
case Zero => "0"
case One => "1"
case Elem(x: Int) => x.toString
case Add(x, y) => x + " + " + y
case Mult(x, y) => x + " * " + y
}
hylo(findDivisorsOf)(prettyPrint)(ringFunctor)(12)
---
res44: String = "3 * 2 * 2"
Nice! We are using all our abstract functions to get pretty nice functionalities.
Morphisms between inductive structures
We are going to end this talk with one last comment about inductive structures. We have already seen functions to evaluate (catamorphism) and to generate (anamorphism) inductive data types. But what happens if we want to use a function between inductive data Types? For instance, a function reduce: Ring => Ring that simplifies expressions as x + x => 2*x. This can be made by using our Fix and a special kind of algebra. The algebra has signature RingF[Fix[RingF]] => Fix[RingF], because we need to work over the general case. Take a look to the implementation of this:
def reduce[A]: RingF[Fix[RingF]] => Fix[RingF] = {
case Add(x, y) => if (x == y) Fix[RingF](Mult(y, Fix[RingF](Elem(2))))
else Fix[RingF](Add(x,y))
case other => Fix[RingF](other)
}
It looks pretty simple. You can compare it with its implementation using our first defined Ring without using Fix:
def reduce: Ring => Ring = {
case Zero => Zero
case One => One
case Elem(x) => Elem(x)
case Add(x, y) => if (x == y) Mult(reduce(x), Elem(2)) else Add(reduce(x), reduce(y))
case Mult(x, y) => Mult(reduce(x), reduce(y))
}
Take a look at the shape of this function. It has a lot of recursive calls in so many places, what is error-prone and, second, its to verbose, because all is the same but for the case Add(x,x). This is one of the advantage of the recursion scheme pattern.
Conclusions and References
We have seen the recursion scheme pattern with a lot of examples. The main functions has been presented but we have left under the hood some details and mathematical justifications of the results. I tried to focus on the intuition and the constantly relation between mathematical diagrams and code, which is a funny way of writing code.
Some references I used to write this post are:
Dar referencias